本题采用涡量-流函数方法求解方腔问题. 本题首先由速度分布来计算初始时刻涡量分布,以及流函数分布,并对涡量进行了一次时间推进即得到ω_(i,j)^2,之后用ω_(i,j)^2对流函数进行迭代计算(只进行一次),这是由于时间推进过程中的中间步无需迭代至收敛,最终收敛即可。由此得到φ_(i,j)^2之后比较φ_(i,j)^2与φ_(i,j)^1的绝对值之差,当φ_(i,j)^(n+1)与φ_(i,j)^n之差小于〖10〗^(-10)时停止循环,反之则继续循环迭代。循环中包括了通过流函数反解出u,v的反解函数,对ω进行时间推进的涡量推进函数,以及对φ进行jocabi迭代的jocabi迭代函数
文件列表:
wtuijin.m
zhuchengxu.m
fanjie.m
joc.m
运行例图:
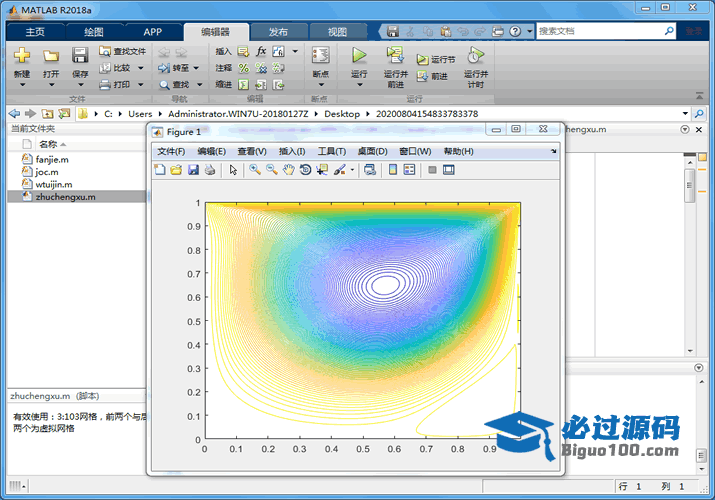
 本题采用涡量-流函数方法求解方腔问题.rar
(1.51 KB, 下载次数: 0, 售价: 30 积分)
本题采用涡量-流函数方法求解方腔问题.rar
(1.51 KB, 下载次数: 0, 售价: 30 积分)
|